NUMERICAL STUDY OF DOUBLE CATTANEO-CHRISTOV DIFFUSION EFFECTS IN MHD 3-DIMENSIONAL CASSON FLUID FLOW PAST AN EXPONENTIALLY STRETCHING SHEET
DOI:
https://doi.org/10.15421/jchemtech.v33i2.314887Keywords:
Three dimensional; Exponentially stretching sheet; Casson fluid; Magnetic field; Nanofluid; Cattaneo-Christov double diffusion: Runge Kutta method; Shooting technique:Abstract
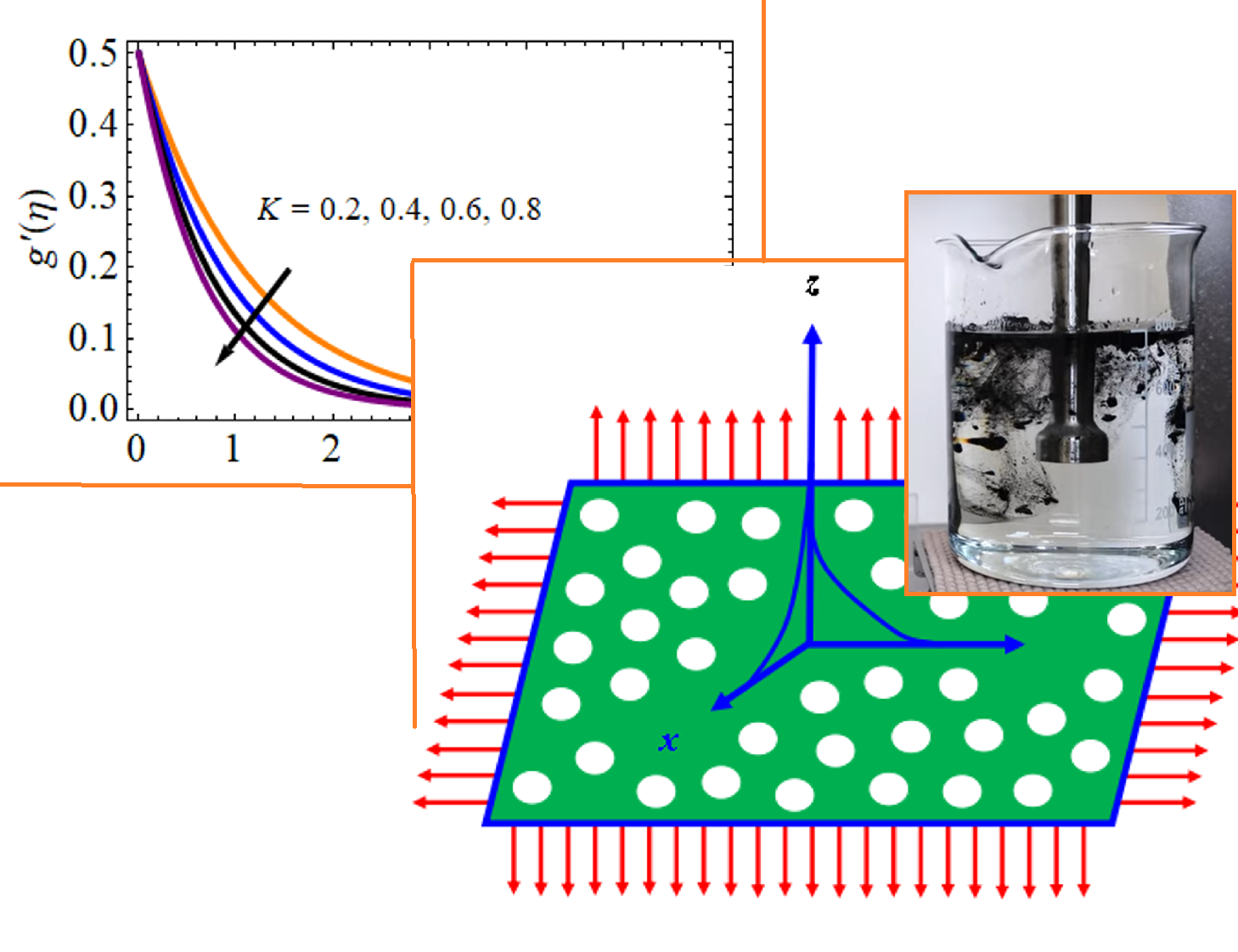
A numerical study of a three-dimensional steady-state flow of a viscous incompressible Casson fluid containing nanofluid particles interacting with a stretching sheet is the primary focus of this work. The equations for concentration and energy include the Cattaneo-Christov double diffusion effects. The Prandtl number plays a crucial role in assessing heat transfer characteristics in fluids. Within nanofluid dynamics, Brownian motion and thermophoresis significantly influence thermal behavior. The Cattaneo-Christov double-diffusion model extends traditional energy and concentration equations by incorporating thermal and solutal relaxation times. Transforming partial differential equations into ordinary differential equations is achieved through appropriate similarity variables. Numerical solutions are obtained using the finite element method to analyze modified governing equations. Graphical representations illustrate the impact of key parameters on velocity, temperature, and concentration profiles. Additionally, computational results evaluate skin friction, Nusselt number, and Sherwood number to quantify heat and mass transfer rates. These insights contribute to advancements in thermal engineering and nanofluid research, offering valuable applications for scientists and engineers working on enhanced heat transfer systems.
References
Nadeem, S., Lee, C. (2016). Series solution of magneto-hydrodynamic boundary layer flow over bi-directional exponentially stretching surfaces, J. Braz. Soc. Mech. Sci. Eng., 38(2), 443–453. https://doi.org/10.1007/s40430-015-0344-2
Sadiq, M.A., Nadeem, S. (2015). Unsteady MHD boundary layer flow of a couple stress nano fluid over a stretching/shrinking surface with convective boundary condition, J. Comput. Theor. Nanosci., 12(11), 4408–4414.
Akbar, N., Khan, Z., Nadeem, S., Khan, W. (2016). Double-diffusive natural convective boundary-layer flow of a nanofluid over a stretching sheet with magnetic field Int. J. Numer. Methods Heat Fluid Flow, 26(1), 108–121.
Hussain, S., Rasheed, K., Ali, A., Vrinceanu, N., Alshehri, A., Shah, Z. (2022). A sensitivity analysis of MHD nanofluid flow across an exponentially stretched surface with non-uniform heat flux by response surface methodology. Sci. Rep., 12, 18523. https://doi.org/10.1038/s41598-022-22970-y
Ali, A., Khan Marwat, D.N., Ali, A. (2022). Analysis of flow and heat transfer over stretching/shrinking and porous surfaces. J. Plast. Film Sheeting Plast. Film Sheeting 38(1), 21–45. https://doi.org/10.1177/87560879211025
Hsiao, K.L. (2016). Stagnation electrical MHD nanofluid mixed convection with slip boundary on a stretching sheet. Appl. Therm. Eng. 98, 850–886
Awais, M., Hayat, T., Ali, A., Irum, S. (2016). Velocity, thermal and concentration slip effects on a magneto-hydrodynamic nanofluid flow. Alex. Eng. J., 55(3), 2107–2114.
Khashiie, N.S., Arifin, N.M., Pop, I., Nazar, R., Hafidzuddin, E.H., Wahi, N. (2020). Three-dimensional hybrid nanofluid flow and heat transfer past a permeable stretching/shrinking sheet with velocity slip and convective condition. Chin. J. Phys., 66, 157–171. https://doi.org/10.1016/j.cjph.2020.03.032
Makinde, O.D., Aziz, A. (2011). Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int. J. Therm. Sci. 50(7), 1326–1332.
Khan, W.A., Pop, I. (2010). Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf., 53, 2477–2483.
Cattaneo, C. (1948). Sulla conduzione del calore, AttiSemin. Mat. Fis. Univ. Modena Reggio Emilia, 3, 83–101.
Ciarletta, M., Straughan, B. (2010). Uniqueness and structural stability for the Cattaneo-Christov equations, Mech. Res. Commun., 37(5), 445–447.
Mustafa, M. (2015). Cattaneo-Christov heat flux model for rotating flow and heat transfer of upper-convected Maxwell fluid, AIP Adv., 5(4), 047109. https://doi.org/10.1063/1.4917306
Straughan, B. (2010). Thermal convection with the Cattaneo-Christov model, Int. J. Heat Mass Transfer, 53(1), 95–98.
Han, S., Zheng, L., Li, C., Zhang, X. (2014). Coupled flow and heat transfer in viscoelastic fluid with Cattaneo-Christov heat flux model, Appl. Math. Lett., 38, 87–93.
Hayat, T., Khan, M.I., Farooq, M., Alsaedi, A., Waqas, M., Yasmeen, T. (2016). Impact of Cattaneo-Christov heat flux model in flow of variable thermal conductivity fluid over a variable thicked surface, Int. J. Heat Mass Transfer, 99, 702–710.
Hayat, T., Khan, T., Farooq, M., Yasmeen, T., Alsaedi, A. (2016). Stagnation point flow with Cattaneo-Christov heat flux and homogeneous-heterogeneous reactions, J. Mol. Liq., 220, 49–55. https://doi.org/10.1016/j.molliq.2016.04.032
Farooq, M., Khan, M.I., Waqas, M., Hayat, T., Alsaedi, A., Khan, M.I. (2016). MHD stagnation point flow of viscoelastic nanofluid with non-linear radiation effects, J. Mol. Liq., 221, 1097–1103.
Hayat, T., Bashir, G., Waqas, M., Alsaedi, A. (2016). MHD flow of Jeffrey liquid due to a nonlinear radially stretched sheet in presence of Newtonian heating, Results Phys., 6, 817–823.
Afzal, K. Aziz, A. (2016). Transport and heat transfer of time dependent MHD slip flow of nanofluids in solar collectors with variable thermal conductivity and thermal radiation, Results Phys., 6, 746–753.
Gundagani, M., Babu, N.V.N., Gadially, D. S. Bhati, M. Sanjay, Ch., Nirmala Kasturi, V.. (2024). Study of Nano-Powell-Erying fluid flow past a porous stretching sheet by the effects of MHD, thermal and mass convective boundary conditions. J. Umm Al-Qura Univ. Eng. Archit. https://doi.org/10.1007/s43995-024-00056-2
Murali, G., Deepa, G., Kasturi, N. V., Poornakantha, Т. (2023). Joint effects of thermal diffusion and diffusion thermo on MHD three dimensional nanofluid flow towards a stretching sheet, Mathematical models in engineering,9(4),130143,https://doi.org/10.21595/mme.2023.23590.
Gundagani, M., Mamidi, L.P., Tanuku, P.K. (2024). Finite element solutions of Double diffusion effects on three-dimensional MHD Nano-Powell-Erying fluid flow in presence of thermal and mass Biot numbers. J. Eng. Appl. Sci., 71, 9. https://doi.org/10.1186/s44147-023-00347-w
Murali, G., Babu, N.V.N. (2023). Convective MHD Jeffrey Fluid Flow Due to Vertical Plates with Pulsed Fluid Suction:A Numerical Study, Journal of computational applied mechanics, 54(1), 36–48. doi: 10.22059/JCAMECH.2023.351326.773.
Mebarek-Oudina, F., Dharmaiah, G., Rama Prasad, J. L., Vaidya, H., Kumari, Thermal, M. A. (2025). Flow Dynamics of Magnetohydxrodynamic Burgers' Fluid Induced by a Stretching Cylinder with Internal Heat Generation and Absorption, International Journal of Thermophysics, 25, 100986. https://doi.org/10.1016/j.ijft.2024.100986
Kirubaharan, D.R., Subhashini, A.D., Murali, G. (2024). Study of Three Dimensional Casson-Nanofluid Flow due to a Linear Porous Stretching Sheet in the Presence of Double Diffusion Effects, Advances in Systems Science and Applications, 24(3), 90–103. https://doi.org/10.25728/assa.2024.2024.03.1539
Murali, G., Deepa, G., Venkata Madhu, J., Nirmala Kasturi, V., Bhati, S.M., Narendra Babu, N. (2025). Three Dimensional Chemically Reacting Oldroyd-B Fluid + Nanofluid Flow in Presence of Thermophoresis and Brownian Motion Effects, Discontinuity, Nonlinearity, and Complexity, 14(2), 373–388. https://doi.org/10.5890/DNC.2025.06.010
Tanuku, P.K., Mamidi, L.P., Gundagani, M. (2024). Modelling and analysis of three-dimensional chemically reacting, radiating Casson-nanofluid flow: thermophoresis and Brownian motion effects, Acta Polytechnica, 64(5), 455–463. https://doi.org/10.14311/AP.2024.64.0455
Murali, G., Lakshmi, P., Amarnath, M. (2025). Three-dimensional MHD flow of a radiative Eyring–Powell nanofluid: Exploring Hall effects and heat transfer. Theor Math Phys., 223, 1070–1086. https://doi.org/10.1134/S0040577925060170
Murali, G., Venkata Madhu, J., Deepa, G. (2025). Hall current and MHD impacts on a 3D Maxwell nanofluid flow across a porous stretching surface. Theor Math Phys 223, 899–914. https://doi.org/10.1134/S0040577925060030
Anil Kumar, M., Mebarek-Oudina, F., Mangathai, P., Shah, N. A., Vijayabhaskar, N., Venkatesh, Ch., Fouad, Y. (2025). The Impact of Soret Dufour and Radiation on the Laminar Flow of a Rotating liquid past a Porous plate via Chemical Reaction, Modern Physics Letters B, 39(10), 2450458. https://doi.org/10.1142/S021798492450458X
Rajesh, V, Sheremet, M. (2023). Free Convection in a Square Ternary Hybrid Nanoliquid Chamber with Linearly Heating Adjacent Walls. Nanomaterials, 13(21). https://doi.org/10.3390/nano13212860
Khan, Y, Majeed, AH, Shahzad H. (2022). Numerical Computations of Non-Newtonian Fluid Flow in Hexagonal Cavity With a Square Obstacle: A Hybrid Mesh–Based Study. Front Phys., 10. https://doi.org/10.3389/fphy.2022.891163
F. Mebarek-Oudina, M. Bouselsal, N. Biswas, H. Vaidya, K. Ramesh, Heat transfer in a zigzag wall cavity and different obstacles filled with MgO-SWCNT/water hybrid nanofluids, Modern Physics Letters B, (2025) 2550163. https://doi.org/10.1142/S0217984925501635
Raza, J., Mebarek-Oudina, F., Ali, H., Sarris, I. E. (2024). Slip effects on Casson Nanofluid over a Stretching sheet with activation energy: RSM Analysis, Frontiers in Heat and Mass Transfer, 22(4), 1017–1041. https://doi.org/10.32604/fhmt.2024.052749
Ould Said, B., Mebarek-Oudina F., Medebber, M. A. (2024) Magneto-hydro-Convective Nanofluid flow in Porous Square Enclosure, Frontiers in Heat and Mass Transfer, 22(5), 1343–1360. https://doi.org/10.32604/fhmt.2024.054164
Ramesh, K. Mebarek-Oudina, F. Souayeh, B. (2023). Mathematical Modelling of Fluid Dynamics and Nanofluids, 1st edition, CRC Press (Taylor & Francis). https://doi.org/10.1201/9781003299608
Mebarek-Oudina, F. (2025). CFD Simulation: Thermo-Fluids and Nanofluids in Engineering and Biomedicine, 1st edition, De-Gruyter. https://doi.org/10.1515/9783111405094
Mezaache, A., Mebarek-Oudina, F., Vaidya, H., Fouad, Y. (2024). Heat Transfer Analysis of Nanofluid Flow with Entropy generation in a Corrugated Heat Exchanger Channel Partially filled with Porous Medium. Heat Transfer, 53(8), 46254647. https://doi.org/10.1002/HTJ23149.
Gupta, T., Pandey, A. K., Kumar, M. (2023). Effect of Thompson and Troian slip on CNT-Fe3O4/kerosene oil hybrid nanofluid flow over an exponential stretching sheet with Reynolds viscosity model. Mod. Phys. Lett. B, 2350209. doi:10.1142/S0217984923502093
Poornakantha, T., Laksmiprsanna, M., Murali, G. (2025). Modelling and Analysis of Three-Dimensional Maxwell-Nanofluid Flow over a Bi-Directional Stretching Surface in the Presence of a Magnetic Field. International Journal for Engineering Modelling, 38(1), 53–72. https://doi.org/10.31534/engmod.2025.1.ri.04d.
Sivaiah, S., Gundagani, M., Karanamu, M. P. (2012). Analysis of Heat and Mass Transfer Effects on an Isothermal Vertical Oscillating Plate. Walailak J. Sci. Tech., (WJST), 9(4), 407–415.
Murali, G., Venkata Madhu, J., Deepa, G., Suresh, P., Nagaraju, B. (2025). Three-Dimensional Oldroyd-B Fluid Flow Past a Stretching Surface with Magnetic Field, Nanofluid Particles and Cattaneo-Christov Double Diffusion Effects, Johnson Matthey Technology Review, 69(2), 299–320. https://doi.org/10.1595/205651325X17375408788409.
Gundagani, M., Javvaji, V. Gadipalli, D. Pallerla, S. Al-Mdallal Q., Bhati, S. (2025). A Numerical Study on MHD 3-D Casson-Nanofluid Flow Past an Exponentially Stretching Sheet with Double Cattaneo-Christov Diffusion Effects, Rev. int. métodos numér. cálc. diseño ing., 41(2), 21.
Nadeem, S., Haq, R. U., Akbar, N. S., Khan, Z. H. (2013). MHD three-dimensional Casson fluid flow past a porous linearly stretching sheet. Alexandria Engineering Journal, 52(4), 577–582. https://doi.org/10.1016/j.aej.2013.08.005 .
Downloads
Published
Issue
Section
License
Copyright (c) 2025 Oles Honchar Dnipro National University

This work is licensed under a Creative Commons Attribution 4.0 International License.
- Authors reserve the right of attribution for the submitted manuscript, while transferring to the Journal the right to publish the article under the Creative Commons Attribution License. This license allows free distribution of the published work under the condition of proper attribution of the original authors and the initial publication source (i.e. the Journal)
- Authors have the right to enter into separate agreements for additional non-exclusive distribution of the work in the form it was published in the Journal (such as publishing the article on the institutional website or as a part of a monograph), provided the original publication in this Journal is properly referenced
- The Journal allows and encourages online publication of the manuscripts (such as on personal web pages), even when such a manuscript is still under editorial consideration, since it allows for a productive scientific discussion and better citation dynamics (see The Effect of Open Access).