TEMPERATURE WAVES METHOD FOR MODELING REGENERATIVE HEAT EXCHANGERS
DOI:
https://doi.org/10.15421/jchemtech.v31i1.269522Keywords:
regenerative heat exchangers, heat regenerators, modeling, air-to-air heat exchanger.Abstract
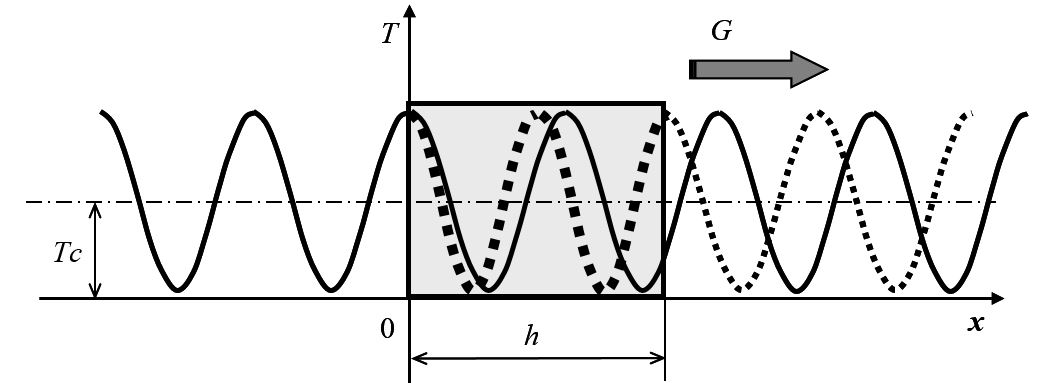
Regenerative heat exchangers have a large surface area per unit volume and low cost, compared with other types of heat exchangers. The complexity of their proper design and optimization is one of the reasons why these devices are not widely used. The article describes a temperature-wave approach to the modeling of heat regenerators. The verification of the novel temperature wave’s model was held by the experimental data of the regenerator used in ventilation systems. The temperature waves method for computation of a heat regenerator makes it possible to take into account the influence of the following factors: the variable gas temperature at the regenerator’s inlet, processes of non-stationary heat conduction in the elements of packing, the longitudinal thermal conductivity of the packing. Despite a complex mathematical apparatus used to justify the method of temperature waves for designing regenerators, the very procedure for calculating such a heat exchanger has proven to be relatively simple and convenient for computer calculations.
References
Nusselt, W. (1927). Die theorie des winderhitzers. In V.D.I; Zeitschrift des Vereines deutscher Ingenieure, 71, 85–91.
Hausen, H. (1929). Über Die Theorie Des Wärmeaustausches in Regeneratoren. Z. Angew. Math. und Mech, 9, 173–200.
Hausen, H. (1981). [Heat transfer with counterflow, forward flow and cross current], Moscow: Energoatomizdat (in Russian).
Bahnke, G. D, Howard, C.P. (1964). The effect of longitudinal heat conduction on periodic-flow heat exchangers performance. Trans ASME J Eng Power, 86(2), 105–117.
Kilkovský, B. (2020). Review of Design and Modeling of Regenerative Heat Exchangers. Energies, 13, 759.
Sadrameli, S. M. (2016). Mathematical models for the simulation of thermal regenerators: A state-of-the-art review. Renewable and Sustainable Energy Reviews, 58, 462–476.
Kravchenko, M.B. (2010). [Analytical study of counterflow heat exchangers]. Tekhnicheskiye gazy, 5, 24–30 (in Russian).
Kravchenko, M. B. (2014). [Wave approach to modeling periodic heat transfer processes]. Tekhnicheskiye gazy, 6, 20–27 (in Russian).
Kravchenko, M. B. (2014). [Wave adsorption]. Saarbrücken: Lap. Lambert Academic Publishing (in Russian).
Lavrenchenko, G. K., Kravchenko M. B. (2019). The characteristics of a 4 K Gifford-McMahon cryocooler with a second stage-regenerator packed with cenospheres. Low Temp. Phys, 45, 452–464.
Mikusinsky, Yan. (1956). [Operator calculus]. Moscow: From foreign literature. (in Russian).
Lykov, A. V. (1978). [Heat and Mass Transfer]. Moscow: Energia. (in Russian).
Kartashov, E. M. (1985). [Analytical methods in the theory of thermal conductivity of solids]. Moscow: Vysshaya shkola (in Russian).
Nizovtsev, M. I., Borodulin, V. Yu., Letushko, V. N., Zakharov, A. A. (2016). Analysis of the efficiency of air-to-air heat exchanger with a periodic change in the flow direction. Applied Thermal Engineering, 93, 113–121.
Ramin, H., Krishnan, E. N., Gurubalan, A., Alabi, W. O., Simonson, C. J. (2019). Transient sensor errors and their impact on fixed-bed regenerator (FBR) testing
standards. in: 27th Can. Congr. Appl. Mech., MDPI. Sherbrooke. 1–6.
Ramin, H., Krishnan, E. N., Alabi, W., Simonson C. J. (2020). Temperature Measurement Correction for the Determination of the Effectiveness of Fixed-Bed Regenerators (FBRs) for HVAC Applications. in: 2020 ASHRAE Annu. Summer Conf., ASHRAE. Austin.
Ramin H., Krishnan E. N., Gurubalan A., Alabi W. O., Simonson C. J. (2020). Transient sensor errors and their impact on fixed-bed regenerator (FBR) testing standards. Science and Technology for the Built Environment. 3(27), 1–22.
Krishnan E. N., Ramin H., Shakourib M., Wilsonc L. D., Simonsona C. J. (2020). Development of a small-scale test facility for effectiveness evaluation of fixed-bed regenerators. Applied Thermal Engineering, 174, 115263.
Downloads
Published
Issue
Section
License
Copyright (c) 2023 Oles Honchar Dnipro National University

This work is licensed under a Creative Commons Attribution 4.0 International License.
- Authors reserve the right of attribution for the submitted manuscript, while transferring to the Journal the right to publish the article under the Creative Commons Attribution License. This license allows free distribution of the published work under the condition of proper attribution of the original authors and the initial publication source (i.e. the Journal)
- Authors have the right to enter into separate agreements for additional non-exclusive distribution of the work in the form it was published in the Journal (such as publishing the article on the institutional website or as a part of a monograph), provided the original publication in this Journal is properly referenced
- The Journal allows and encourages online publication of the manuscripts (such as on personal web pages), even when such a manuscript is still under editorial consideration, since it allows for a productive scientific discussion and better citation dynamics (see The Effect of Open Access).