THE METHOD OF CALCULATING THE DISSIPATION ENERGY DURING THE FLOW OF A GENERALIZED-DISPLACED FLUID IN THE CHANNELS OF TECHNOLOGICAL EQUIPMENT
DOI:
https://doi.org/10.15421/jchemtech.v31i2.277115Keywords:
fluid; generalized-displaced; dissipation; flow; channel; calculation.Abstract
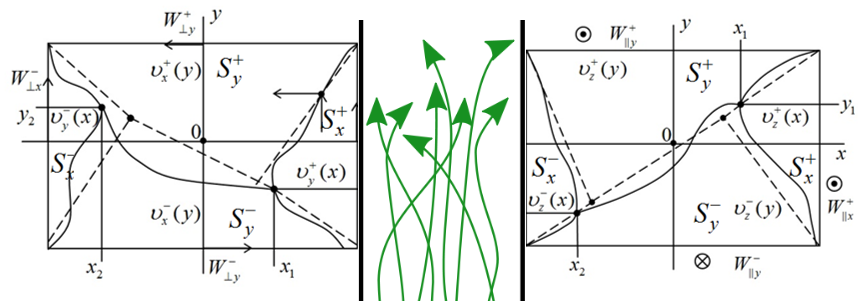
This paper considers the problem of determining the dissipation energy during the flow of a generalized-displaced fluid in the channels of technological equipment. It is known that during the flow of highly viscous non-Newtonian fluids, the problem of heating this substance arises. This is primarily due to the fact that during the transportation of the material, the dissipation mechanism takes place, which leads to overheating of the material. In its turn, this affects the changes in the physical and chemical properties of the material and the technical and economic indicators of the corresponding equipment. We propose a method for calculating the dissipation energy during the flow of a generalized-displaced fluid in the channels of screw machines. To solve this problem, we used the superposition method to construct fields of larger dimensions from fields of smaller dimensions with different boundary conditions. A channel of flat and rectangular shape is considered. Fluid movement is carried out in the longitudinal and longitudinal-transverse directions of the channel. To calculate the amount of energy dissipation of a generalized-displaced fluid, it is necessary to first divide the channel sections into sections with different expressions for the flow rate. At the same time, each of the subareas consists of two curvilinear triangles and one rectangle. The mandatory steps of the calculations are the breakdown of the rectangle of the cross section of the straight channel, and the calculation of the integrals from the derivatives of the velocity. The proposed method allows to calculate the energy of dissipative heat generation when calculating the optimal parameters of technological equipment.
References
Berk, Z. (2009). Food Process Engineering and Technology. Israel. Elsevier Department of Biotechnology and Food Engineering Israel Institute of Technology.
Harlamov S. (2013). [Hydrodynamics and heat exchange: new trends and perspective modeling of internal flows]. LAP LAMBERT Academic Publishing. (in Russian).
Gale, M. (2009). Mixing in Single Screw Extrusion. USA: Smithers Rapra Press.
Ulyev, L. M. (2016). [Laminar flow in coaxial conical channels]. Kharkiv. Ukraine: NTU "KhPI". (in Ukraine).
Ferziger, J. Peric M. (2002) Computational Methods for Fluid Dynamics. Berlin, Germany, Springer. (in English).
Anandha, Rao M. (2014). Rheology of Fluid, Semisolid, and Solid Foods: Principles and Applications. New York, USA: Imprint: Springer.
Tanner, R. I. (2002). Engineering Rheology. New York, USA: Oxford University Press.
Yahno, O. M. & Zhelyak, V. I. (1995). Hydraulics of non-Newtonian fluids. Educational manual. Kiev: Vischa shkola (in Ukrainian).
Haldenwang, R., Slatter, P.T. and Chhabra, R.P. (2010) An experimental study of non-Newtonian fluid flow in rectangular flumes in laminar, transition and turbulent flow regimes. Journal of the South African Institution of Civil Engineering, 52(1), 11-19.
Тovazhnyansky, L. L., Biletsky, E.V., Tolchinsky Yu. A. (2013) [Modeling of flows of non-Newtonian fluids in channels of basic geometry]. Kharkiv. Ukraine: NTU "KhPI". (in Ukraine).
Astarita, Dzh., Marruchi, Dzh. (1978). [Fundamentals of the hydromechanics of non-Newtonian fluids]. Moscow: Mir (in Russian).
Morrison, F.A, (2001) Understanding Rheology, New York, USA: Oxford University Press.
Cantelli, A. (2009). [Uniform Flow of Modified Bingham Fluids in Narrow Cross Sections]. Journal of Hydraulic Engineering, 135(8), 640–50. https://doi.org/10.1061/7900.0000092
Baptista, A., Alves, M.A., Coelho, P.M. (2014). [Heat transfer in fully developed laminar flow of power law fluids]. Journal of Heat Transfer, 136(4), 1–8. https://doi.org/110.1115/1.4025662
Vlachopoulos, J. Fundamentals of Fluid Mechanics., Dundas, Canada: Polydynamics inc.
Golovanchikov, A. B., Shagarova, A. A. (2015) [Modeling the flow of a viscoplastic reaction mass in a screw reactor with a low viscosity wall layer]. Izvestiya vuzov. Khimiya i khimicheskaya tekhnologiya. 58(12), 69–72. https://doi.org/10.1134/S1070427209040405
Ternik P., Marn J., Zuni Z., (2006). Non-Newtonian fluid flow through a planar symmetric expansion: Shear-thickening fluids, J. Non-Newtonian Fluid Mech., 135, 136–148
Letelier, M. F., Hinojosa, C. B., Siginer, D. A. (2017). Analytical solution of the Graetz problem for non-linear viscoelastic fluids in tubes of arbitrary cross-section. International Journal of Thermal Sciences ,111, 369–378.
Shahbani-Zahiri, A. (2018) "Numerical simulation of inertial flow of heated and cooled viscoelastic fluids inside a planar sudden expansion channel: investigation of stresses effects on the total dissipation." Meccanica 53(11-12), 2897–2920.
Frank-Kamenetskii, D.A. (2015) Diffusion and Heat Exchange in Chemical Kinetics. Princeton. USA: Princeton University Press.
Mitsoulis, E., Tsamopoulos, J., (2017). Numerical simulations of complex yield-stress fluid flows. Rheologica Acta, 56. 231–258.
Toth, G., Bata, A., Belina, K. (2018). Determination of polymer melts flow-activation energy a function of wide range shear rate. IOP Conf. Series: Journal of Physics. 1045.
Petrenko, E., Biletsky, E., Ryshchenko, I. Semeniuk, D. (2021). Equation of heat exchange during the flow of non-newtonian fluids in channels of technological equipment. Journal of Chemistry and Technologies. 29(2), 254–264. https://doi.org/10.15421/jchemtech.v29i2 229829
Biletsky, E. Semeniuk, D. (2012). Method of determining of dissipation energy during the movement of Bingham fluid. Journal of technical university of Moldova and moldovian engineering association. Meridian engineresc. 4, 40–44.
Biletsky, E. Petrenko, E., Semeniuk, D. (2016). Three-dimensional model of non-Newtonian fluid flow in the rectangular channel. Ukrainian Food Journal. 5(3), 550–560. https://doi.org/10.24263/2304-974X-2016-5-3-14
Petrenko, E., Biletsky, E., Semeniuk, D. (2019). Modeling of the viscoplastic flow of a bingam fluid with transverse circulation in a rectangular channel of a worm machine. Journal of Chemistry and Technologies. 27(2), 550–560. https://doi.org/10.15421/081921
Petrenko, E., Biletsky, E., Semeniuk, D. (2020). Determination of heat transfer coefficients during the flow of non-Newtonian fluids in pipes and channels of chemical process equipment. Journal of Chemistry and Technologies. 28(1), 88–99. https://doi.org/10.15421/082010
Petrenko, E., Biletsky, E., Semeniuk, D. (2020). Simulation of the flow of viscous-plastic barotropic compressible material in channels of complex geometry. Journal of Chemistry and Technologies. 30(2), 275–284. https://doi.org/10.15421/.255960
Biletsky, E. Petrenko, E., Semeniuk, D. (2014). Theoretical aspects of non-newtonian fluids flow simulation in food technologies. Ukrainian Food Journal. 3(2), 271–280.
Downloads
Published
Issue
Section
License
Copyright (c) 2023 Oles Honchar Dnipro National University

This work is licensed under a Creative Commons Attribution 4.0 International License.
- Authors reserve the right of attribution for the submitted manuscript, while transferring to the Journal the right to publish the article under the Creative Commons Attribution License. This license allows free distribution of the published work under the condition of proper attribution of the original authors and the initial publication source (i.e. the Journal)
- Authors have the right to enter into separate agreements for additional non-exclusive distribution of the work in the form it was published in the Journal (such as publishing the article on the institutional website or as a part of a monograph), provided the original publication in this Journal is properly referenced
- The Journal allows and encourages online publication of the manuscripts (such as on personal web pages), even when such a manuscript is still under editorial consideration, since it allows for a productive scientific discussion and better citation dynamics (see The Effect of Open Access).