A FIRST-PRINCIPLES STUDY EFFECT PRESSURE OF ELECTRONIC AND OPTICAL PROPERTIES OF R-TiO2
DOI:
https://doi.org/10.15421/jchemtech.v32i1.289257Keywords:
first principle; Ultrasoft pseudopotential; Density of states; Refractive index; Hydrostaticpressure.Abstract
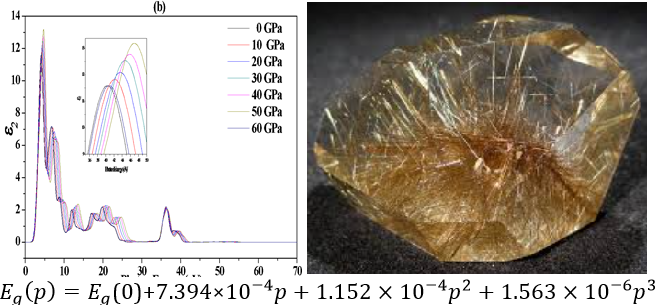
The band structure, density of state, and optical properties of TiO2 rutile were studied using first principles calculations within the framework of density functional theory using the generalized gradient approximation (GGA-RPBE) at both zero and high pressures. we used the Birch-Murnaghan equation of state calculate of volume and bulk modulus by approximation that we mentioned above and our results were compared with previous theoretical and experimental data, we noticed a good agreement between the results. The band gap of 2.098 eV (GGA) remains unchanged when the pressure is increased from 0 to 10 GPa, indicating an underestimation. The reduction in volume and lattice constants with increasing pressure is responsible for the decrease in band gap. There is a good agreement between the experimental results and the dielectric constant ε (ω) and refractive index. The photocatalytic activity of TiO2 is found to decrease with increasing pressure based on the absorption spectrum. The energy loss spectra show new peaks as a result of the pressure effect on the energy loss function. From our results, we noticed the effect of pressure within the range (0–60 GPa) on each of the structural, electronic and optical properties, and there is also good agreement between the current results and previous results.
References
Diebold, U. (2003). The surface science of titanium dioxide. Surface science reports, 48(5-8), 53-229. https://doi.org/10.1016/S0167-5729(02)00100-0
Long, L. L., Zhang, A. Y., Yang, J., Zhang, X., Yu, H. Q. (2014). A green approach for preparing doped TiO2 single crystals. ACS Applied Materials & Interfaces, 6(19), 16712–16720. https://doi.org/10.1021/am503661w
Azer, B. B., Gulsaran, A., Pennings, J. R., Saritas, R., Kocer, S., Bennett, J. L., Yavuz, M. (2022). A Review: TiO2 based photoelectrocatalytic chemical oxygen demand sensors and their usage in industrial applications. Journal of Electroanalytical Chemistry, 918, 116466. https://doi.org/10.1016/j.jelechem.2022.116466
Varghese, O. K., Grimes, C. A. (2003). Metal oxide nanoarchitectures for environmental sensing. Journal of nanoscience and nanotechnology, 3(4), 277–293. https://doi.org/10.1166/jnn.2003.158
Lazzeri, M., Vittadini, A., Selloni, A. (2001). Structure and energetics of stoichiometric TiO2 anatase surfaces. Physical Review B, 63(15), 155409. https://doi.org/10.1103/PhysRevB.63.155409
Nie, X., Zhuo, S., Maeng, G., & Sohlberg, K. (2009). Doping of TiO2 Polymorphs for Altered Optical and Photocatalytic Properties. International Journal of Photoenergy, 2009. https://doi.org/10.1155/2009/294042
Zaleska, A. (2008). Doped-TiO2: a review. Recent patents on engineering, 2(3), 157–164. https://doi.org/10.2174/187221208786306289
Henderson, M. A. (2011). A surface science perspective on TiO2 photocatalysis. Surface Science Reports, 66(6-7), 185–297. https://doi.org/10.1016/j.surfrep.2011.01.001
Labat, F., Baranek, P., Domain, C., Minot, C., & Adamo, C. (2007). Density functional theory analysis of the structural and electronic properties of TiO2 rutile and anatase polytypes: Performances of different exchange-correlation functionals. The Journal of chemical physics, 126(15). https://doi.org/10.1063/1.2717168
Morita, K., Yasuoka, K. (2018). Density functional theory study of atomic and electronic properties of defects in reduced anatase TiO2 nanocrystals. AIP Advances, 8(3). https://doi.org/10.1063/1.5021024
Islam, M. M., Bredow, T., Gerson, A. (2007). Electronic properties of oxygen-deficient and aluminum-doped rutile TiO2 from first principles. Physical Review B, 76(4), 045217. https://doi.org/10.1103/PhysRevB.76.045217
Fox, H., Newman, K. E., Schneider, W. F., Corcelli, S. A. (2010). Bulk and surface properties of rutile TiO2 from self-consistent-charge density functional tight binding. Journal of chemical theory and computation, 6(2), 499–507. https://doi.org/10.1021/ct900665a
Manzoli, M., Freyria, F. S., Blangetti, N., Bonelli, B. (2022). Brookite, a sometimes under evaluated TiO2 polymorph. RSC Advances, 12(6), 3322-333. https://doi.org/10.1039/D1RA09057G
Zhao, W., Li, Y., Shen, W. (2021). Tuning the shape and crystal phase of TiO2 nanoparticles for catalysis. Chemical Communications, 57(56), 6838–6850. https://doi.org/10.1039/D1CC01523K
Milman, V., Refson, K., Clark, S. J., Pickard, C. J., Yates, J. R., Gao, S. P., Segall, M. D. (2010). Electron and vibrational spectroscopies using DFT, plane waves and pseudopotentials: CASTEP implementation. Journal of Molecular Structure: THEOCHEM, 954(1-3), 22–35. https://doi.org/10.1016/j.theochem.2009.12.040
Gao, S. P., Pickard, C. J., Perlov, A., Milman, V. (2009). Core-level spectroscopy calculation and the plane wave pseudopotential method. Journal of Physics: Condensed Matter, 21(10), 104203. 10.1088/0953-8984/21/10/104203
Segall, M. D., Lindan, P. J., Probert, M. A., Pickard, C. J., Hasnip, P. J., Clark, S. J., Payne, M. C. (2002). First-principles simulation: ideas, illustrations and the CASTEP code. Journal of physics: condensed matter, 14(11), 2717. https://doi.org/10.1088/0953-8984/14/11/301
Hammer, B. H. L. B., Hansen, L. B., Nоrskov, J. K. (1999). Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Physical review B, 59(11), 7413. https://doi.org/10.1103/PhysRevB.59.7413
Wen, J. Q., Zhang, J. M., Chen, G. X., Wu, H., Yang, X. (2018). The structural, electronic and optical properties of Nd doped ZnO using first-principles calculations. Physica E: Low-dimensional Systems and Nanostructures, 98, 168–173. https://doi.org/10.1016/j.physe.2018.01.002
Zhao, W. (2021). A Broyden–Fletcher–Goldfarb–Shanno algorithm for reliability-based design optimization. Applied Mathematical Modelling, 92, 447–465. https://doi.org/10.1016/j.apm.2020.11.012
Wu, S., Luo, X., Long, Y., Xu, B. (2019). Exploring the phase transformation mechanism of titanium dioxide by high temperature in situ method. In IOP Conference Series: Materials Science and Engineering 493(1), 012010. https://doi.org/10.1088/1757-899X/493/1/012010
Birch, F. (1978). Finite strain isotherm and velocities for single‐crystal and polycrystalline NaCl at high pressures and 300 K. Journal of Geophysical Research: Solid Earth, 83(B3), 1257–1268. https://doi.org/10.1029/JB083iB03p01257
Jun, Z., Jing-Xin, Y., Yan-Ju, W., Xiang-Rong, C., & Fu-Qian, J. (2008). First-principles calculations for elastic properties of rutile TiO2 under pressure. Chinese Physics B, 17(6), 2216. https://doi.org/10.1088/1674-1056/17/6/046
Iuga, M., Steinle-Neumann, G., Meinhardt, J. (2007). Ab-initio simulation of elastic constants for some ceramic materials. The European Physical Journal B, 58, 127–133. https://doi.org/10.1140/epjb/e2007-00209-1
Basavaraj, K., Nyayban, A., Panda, S. (2022, July). Structural phase transitions and elastic properties of TiO2 polymorphs: Ab-initio study. In IOP Conference Series: Materials Science and Engineering, 1248(1), 012064. https://doi.org/10.1088/1757-899X/1248/1/012064
Yao, H., Ouyang, L., Ching, W. Y. (2007). Ab initio calculation of elastic constants of ceramic crystals. Journal of the American Ceramic Society, 90(10), 3194–3204. https://doi.org/10.1111/j.1551-2916.2007.01931.x
Zhou, X. F., Dong, X., Qian, G. R., Zhang, L., Tian, Y., Wang, H. T. (2010). Unusual compression behavior of TiO2 polymorphs from first principles. Physical Review B, 82(6), 060102. https://doi.org/10.1103/PhysRevB.82.060102
Al-Khatatbeh, Y., Lee, K. K., Kiefer, B. (2009). High-pressure behavior of TiO 2 as determined by experiment and theory. Physical Review B, 79(13), 134114. https://doi.org/10.1103/PhysRevB.79.134114
Naik, V. M., Haddad, D., Naik, R., Benci, J., Auner, G. W. (2002). Optical properties of anatase, rutile and amorphous phases of TiO2 thin films grown at room temperature by RF magnetron sputtering. MRS Online Proceedings Library (OPL), 755, DD11-12. https://doi.org/10.1557/PROC-755-DD11.12
Perdew, J. P., Levy, M. (1983). Physical content of the exact Kohn-Sham orbital energies: band gaps and derivative discontinuities. Physical Review Letters, 51(20), 1884. https://doi.org/10.1103/PhysRevLett.51.1884
Sham, L. J., Schlüter, M. (1983). Density-functional theory of the energy gap. Physical review letters, 51(20), 1888. https://doi.org/10.1103/PhysRevLett.51.1888
Baizaee, S. M., Mousavi, N. (2009). First-principles study of the electronic and optical properties of rutile TiO2. Physica B: Condensed Matter, 404(16), 2111–2116. https://doi.org/10.1016/j.physb.2009.01.014
Kowalczyk, S. P., McFeely, F. R., Ley, L., Gritsyna, V. T., Shirley, D. A. (1977). The electronic structure of SrTiO3 and some simple related oxides (MgO, Al2O3, SrO, TiO2). Solid State Communications, 23(3), 161–169. https://doi.org/10.1016/0038-1098(77)90101-6
Liu, Q. J., Liu, Z. T., Feng, L. P., Tian, H. (2010). First-principles study of structural, elastic, electronic and optical properties of rutile GeO2 and α-quartz GeO2. Solid state sciences, 12(10), 1748–1755. https://doi.org/10.1016/j.solidstatesciences.2010.07.025
Fang, R. C. (2003). Solid spectroscopy. Chinese Science Technology University Press, Hefei.
Zhang, Y., Shen, W. M. (2005). Basic of solid electronics. Zhe-Jiang University Press, Hangzhou.
Davis, T. A., Vedam, K. (1968). Pressure dependence of the refractive indices of the tetragonal crystals: ADP, KDP, CaMoO4, CaWO4, and rutile. JOSA, 58(11), 1446–1451. https://opg.optica.org/josa/abstract.cfm?URI=josa-58-11-1446
Lide, D. R. (2003). CRC Handbook of Chemistry and Physics, 83rd edn CRC Press, Boca Raton, FL. Nielsen et al.
Ghaleb, A. M., Munef, R. A., Mohammed, S. F. (2022). First principles study the effect of Zn doped MgO on the energy band gap using GGA approximation. Journal of Ovonic Research, 18(1). https://doi.org/10.15251/JOR.2022.181.11
Downloads
Published
Issue
Section
License
Copyright (c) 2024 Oles Honchar Dnipro National University

This work is licensed under a Creative Commons Attribution 4.0 International License.
- Authors reserve the right of attribution for the submitted manuscript, while transferring to the Journal the right to publish the article under the Creative Commons Attribution License. This license allows free distribution of the published work under the condition of proper attribution of the original authors and the initial publication source (i.e. the Journal)
- Authors have the right to enter into separate agreements for additional non-exclusive distribution of the work in the form it was published in the Journal (such as publishing the article on the institutional website or as a part of a monograph), provided the original publication in this Journal is properly referenced
- The Journal allows and encourages online publication of the manuscripts (such as on personal web pages), even when such a manuscript is still under editorial consideration, since it allows for a productive scientific discussion and better citation dynamics (see The Effect of Open Access).